SM2算法功能简述（二） 验签流程

SM2推荐椭圆曲线参数如下：

使用素数域256位椭圆曲线

椭圆曲线方程：y2 = x3 + ax + b

p= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFF

a= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFC

b= 28E9FA9E 9D9F5E34 4D5A9E4B CF6509A7 F39789F5 15AB8F92 DDBCBD41 4D940E93

n= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF 7203DF6B 21C6052B 53BBF409 39D54123

Gx= 32C4AE2C 1F198119 5F990446 6A39C994 8FE30BBF F2660BE1 715A4589 334C74C7

Gy= BC3736A2 F4F6779C 59BDCEE3 6B692153 D0A9877C C62A4740 02DF32E5 2139F0A0

验签流程：

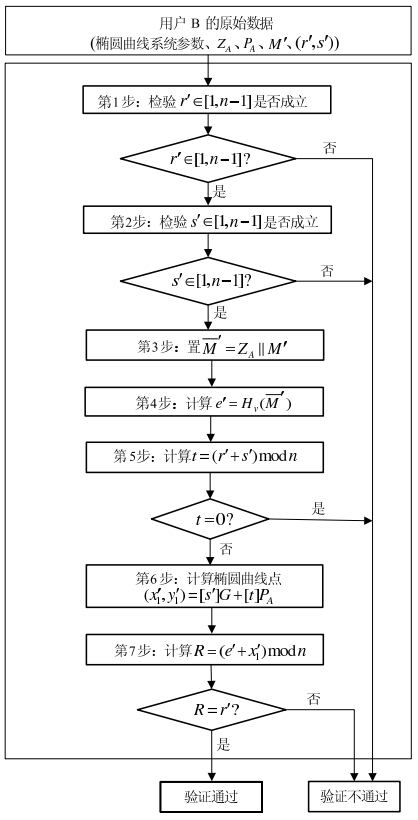
签名验证推导：

sG+[t]PA

=sG+(r+s)PA

=sG+(r+s)dAG（公钥PA=GdA）

=sG+sdAG+rdAG

=(1+dA)sG+rdAG（s=((1+dA)-1 *(k-r*dA)) ）

=(1+dA)(1+dA)−1(k−rdA)G+rdAG   

=(k−rdA)G+rdAG

=kG−rdAG+rdAG

=kG

=(x1,y1)

因为R= (e′ + x′1) mod n，r= ( e + x1 ) mod n，e′和e相等，x′1和x1相等，所以推导出R= r′。